Researchers at Kyoto University have made significant strides in understanding black holes by studying their vibrational characteristics. The team, led by Taiga Miyachi, published their findings in the journal Physical Review D, introducing a novel approach to measuring the complex oscillations known as Quasinormal Modes (QNMs). These vibrations, which occur when black holes are disturbed, provide crucial insights into their mass and shape, especially during mergers.
Exploring Quasinormal Modes
When black holes merge, they produce vibrations that resonate like a bell, revealing details about their structure and dynamics. QNMs are damped oscillations that illustrate how black holes respond to disturbances before settling back into equilibrium. Understanding these modes is vital for advancing gravitational wave astronomy, as they can be detected from Earth when black holes collide.
Measuring the mass of black holes is notoriously challenging. Researchers often rely on the orbital dynamics of nearby stars. QNMs offer a different route to understanding black holes, as they contain fundamental information that depends solely on a black hole’s mass, charge, and angular momentum.
Despite their importance, accurately calculating QNMs poses significant challenges, particularly for rapidly decaying vibrations. The research team employed the Wentzel–Kramers–Brillouin (WKB) method, a mathematical technique still being refined for applications in black hole physics. “To our knowledge, this is the first concrete application of the exact WKB analysis to black hole perturbations,” the authors stated in their paper.
Innovations in Black Hole Research
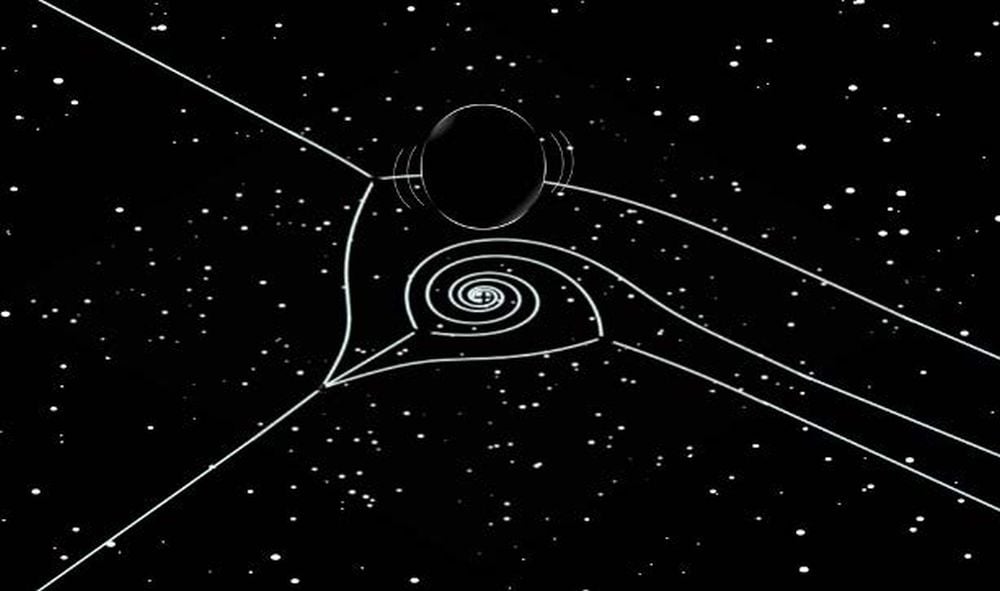
Miyachi expressed pride in applying this method, noting that its mathematical foundations were significantly developed by Japanese mathematicians. The research team successfully tracked wave patterns, revealing intricate structures previously overlooked. They utilized Stokes curves to identify sudden changes in these waves, which are critical for understanding the full picture of QNMs.
“We were surprised at how complex and beautiful the underlying structure of these vibrations turned out to be,” said Miyachi. “We found spiraling patterns in our mathematical analysis that had been missed before, and these turned out to be key in understanding the full picture of quasinormal modes.”
The researchers concluded their paper by emphasizing the versatility of the exact WKB analysis as a powerful tool for addressing black hole perturbation theories across various contexts. This advancement aligns with the notion that mathematics serves as the language of nature, a principle famously championed by Galileo Galilei in his 1623 work, Il Saggiatore (The Assayer).
While much of the intricate mathematics involved may remain inaccessible to the average person, the implications of this research are profound. By employing the WKB method, astrophysicists hope to enhance the accuracy of gravitational wave observatories and deepen our understanding of black holes, those enigmatic giants that play a fundamental role in the universe.